О смерти.

Автор книги «Пять самых распространённых сожалений умирающих»
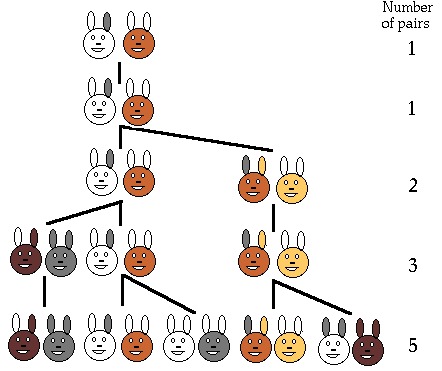
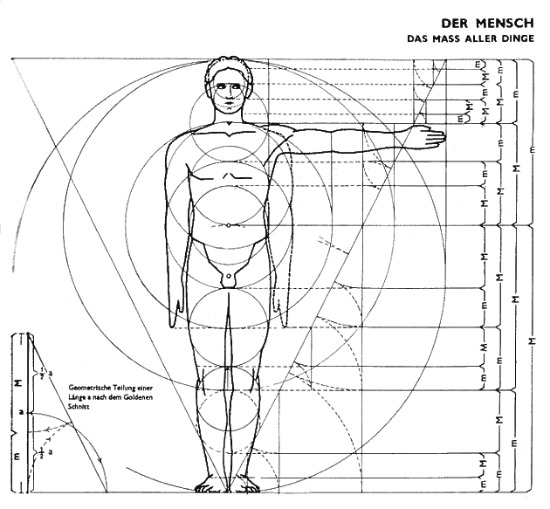
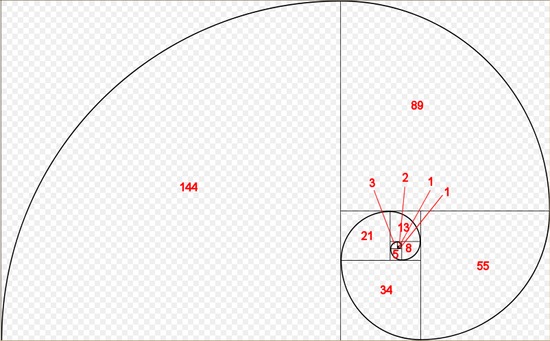
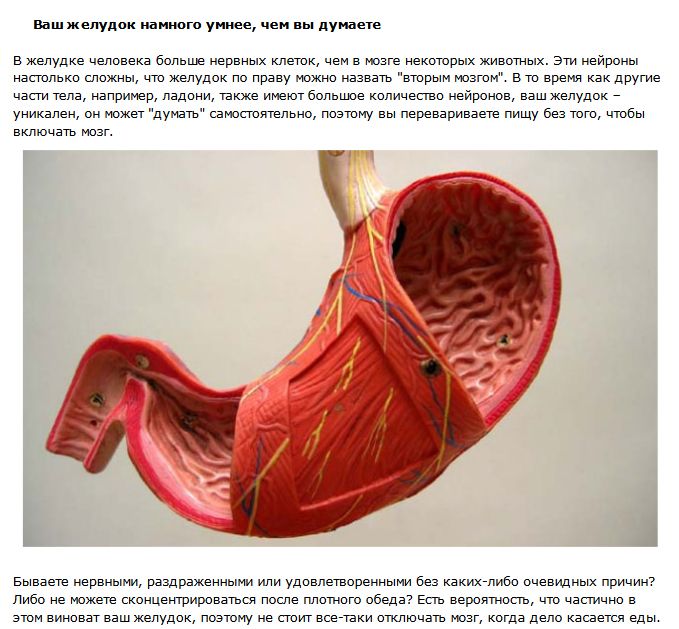
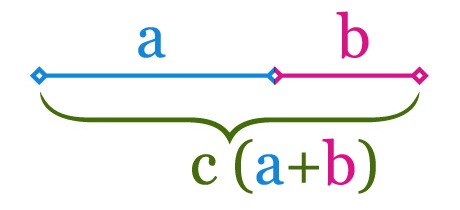Бронни Вее много лет проработала в клинике, ухаживая за людьми,
проживающими последние недели и дни своей жизни.За это время она выслушала много сожалений и, в конце концов, составила список из пяти самых популярных. Вот он:

1. Я жалею, что мне не хватило смелости жить так, как я считал нужным, а не оправдывать ожидания окружающих.

2. Я жалею, что слишком много работал.

3. Я жалею, что мне не хватило смелости выражать свои чувства.

4. Я жалею, что потерял связь с друзьями.

5. Я жалею, что не позволил себе быть счастливее.

Для умирающих это всего лишь сожаления; для тех, у кого ещё есть время что-то исправить, это может стать хорошим уроком.

@темы: Друзья на mail.ru

---

ЗАГАДКИ ПРИРОДЫ И ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ

ЗАГАДКИ ПРИРОДЫ И ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ
( чрезвычайно интересно!)


Леона́рдо Пиза́нский (лат. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи (Fibonacci); о происхождении этого псевдонима имеются разные версии. По одной из них, его отец Гильермо имел прозвище Боначчи («Благонамеренный»), а сам Леонардо прозывался filius Bonacci («сын Благонамеренного»). По другой, Fibonacci происходит от фразы Figlio Buono Nato Ci, что в переводе с итальянского означает «хороший сын родился».
Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. Позже посетил Египет, Сирию, Византию, Сицилию. Леонардо изучал труды математиков стран ислама (таких как ал-Хорезми и Абу Камил); по арабским переводам он ознакомился также с достижениями античных и индийских математиков. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки.
В XIX веке в Пизе был поставлен памятник учёному.


Невозможно представить современный бухгалтерский и вообще финансовый учёт без использования десятичной системы счисления и арабских цифр, начало использования которых в Европе было положено Фибоначчи.
Один из пизанских банкиров, торговавший в Тунисе и занимавшийся там ссудами и откупом налогов и таможенных сборов, некто Леонардо Фибоначчи, применил к банкирскому счетоводству арабские цифры, ознакомив таким образом с ними Европу
Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» (Liber abaci, 1202 год; до наших дней сохранилась только дополненная рукопись 1228 года). Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной. Первые пять глав книги посвящены арифметике целых чисел на основе десятичной нумерации. В VI и VII главе Леонардо излагает действия над обыкновенными дробями. В VIII—X главах изложены приёмы решения задач коммерческой арифметики, основанные на пропорциях. В XI главе рассмотрены задачи на смешение. В XII главе приводятся задачи на суммирование рядов — арифметической и геометрической прогрессий, ряда квадратов и, впервые в истории математики, возвратного ряда, приводящего к последовательности так называемых чисел Фибоначчи. В XIII главе излагается правило двух ложных положений и ряд других задач, приводимых к линейным уравнениям. В XIV главе Леонардо на числовых примерах разъясняет способы приближённого извлечения квадратного и кубического корней. Наконец, в XV главе собран ряд задач на применение теоремы Пифагора и большое число примеров на квадратные уравнения. Леонардо впервые в Европе использовал отрицательные числа, которые рассматривал как долг.
«Книга абака» резко возвышается над европейской арифметико-алгебраической литературой XII—XIV вв. разнообразием и силой методов, богатством задач, доказательностью изложения. Последующие математики широко черпали из неё как задачи, так и приёмы их решения. По первой книге многие поколения европейских математиков изучали индийскую позиционную систему счисления. Другая книга Фибоначчии, «Практика геометрии» (Practica geometriae, 1220 год), содержит
разнообразные теоремы, относящиеся к измерительным методам. Наряду с классическими результатами Фибоначчи приводит свои собственные — например, первое доказательство того, что три медианы треугольника пересекаются в одной точке (Архимеду этот факт был известен, но если его доказательство и существовало, до нас оно не дошло).

В трактате «Цветок» (Flos, 1225 год) Фибоначчи исследовал кубическое уравнение , предложенное ему Иоанном Палермским на математическом состязании при дворе императора Фридриха II. Сам Иоанн Палермский почти наверняка заимствовал это уравнение из трактата Омара Хайяма «О доказательствах задач алгебры», где оно приводится как пример одного из видов в классификации кубических уравнений. Леонардо Пизанский исследовал это уравнение, показав, что его корень не может быть рациональным или же иметь вид одной из квадратичных иррациональностей, встречающихся в X книге Начал Евклида, а затем нашёл приближённое значение корня в шестидесятеричных дробях, равное 1;22,07,42,33,04,40, не указывая, однако, способа своего решения.
«Книга квадратов» (Liber quadratorum, 1225 год), содержит ряд задач на решение неопределённых квадратных уравнений. В одной из задач, также предложенной Иоанном Палермским, требовалось найти рациональное квадратное число, которое, будучи увеличено или уменьшено на 5, вновь даёт рациональные квадратные числа.
Последовательность Фибоначчи, известная всем по фильму "Код Да Винчи" - ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:
Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.


В итоге получается такая последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Эту последовательность можно продолжать бесконечно долго. Её суть в том, что каждое следующее число является суммой двух предыдущих.
У этой последовательности есть ряд математических особенностей, которых обязательно нужно коснуться. Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной,
непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Так отношение какого-либо члена последовательности к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы последовательности через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.
К чему всё это? Так мы приближаемся к одному из самых загадочных явлений природы. Фибоначчи по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.
Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение - высшее проявление совершенства целого и его частей в науке, искусстве и природе.
Если на простом примере, то Золотое Сечение - это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b - 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 2,618, а с к b 1,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.
Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.


Изображение: marcus-frings.de


Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.
Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно

Ничего не напоминает?

Фото: ethanhein on Flickr
И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.
Алое многолистный:

Фото: brewbooks on Flickr
Броколи романеско
Фото: beart.org.uk
Подсолнечник:

Фото: esdrascalderan on Flickr
Сосновая шишка:

Фото: mandj98 on Flickr
А если взглянуть чуть подальше, то можно разглядеть последовательность Фибоначчи в недосягаемых галактиках.


И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.
Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама последовательность далека от совершенства, как и всё в этом мире.
Есть предположение, что последовательность Фибоначчи - это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любой последовательности достаточно знать три её члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.
Каждый член золотой логарифмической последовательности явлется степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: ... z-5; z-4; z-3; z-2; z-1; z0; z1; z2; z3; z4; z5 ... Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: ... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост в последовательности обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.
И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?
Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55...

Источник: greenword.ru
Fibonacci
User:Emijrp/Commons/cs/4
File:Leonardo 1863.jpg
File:Leonardo Fibonacci Estatua.JPG
File:Leonardo da Pisa.jpg

@темы: Друзья на mail.ru

---

ЗАГАДКИ ПРИРОДЫ И ПСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ

ЗАГАДКИ ПРИРОДЫ И ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ
( чрезвычайно интересно!)


Леона́рдо Пиза́нский (лат. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи (Fibonacci); о происхождении этого псевдонима имеются разные версии. По одной из них, его отец Гильермо имел прозвище Боначчи («Благонамеренный»), а сам Леонардо прозывался filius Bonacci («сын Благонамеренного»). По другой, Fibonacci происходит от фразы Figlio Buono Nato Ci, что в переводе с итальянского означает «хороший сын родился».
Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. Позже посетил Египет, Сирию, Византию, Сицилию. Леонардо изучал труды математиков стран ислама (таких как ал-Хорезми и Абу Камил); по арабским переводам он ознакомился также с достижениями античных и индийских математиков. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки.
В XIX веке в Пизе был поставлен памятник учёному.


Невозможно представить современный бухгалтерский и вообще финансовый учёт без использования десятичной системы счисления и арабских цифр, начало использования которых в Европе было положено Фибоначчи.
Один из пизанских банкиров, торговавший в Тунисе и занимавшийся там ссудами и откупом налогов и таможенных сборов, некто Леонардо Фибоначчи, применил к банкирскому счетоводству арабские цифры, ознакомив таким образом с ними Европу
Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» (Liber abaci, 1202 год; до наших дней сохранилась только дополненная рукопись 1228 года). Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной. Первые пять глав книги посвящены арифметике целых чисел на основе десятичной нумерации. В VI и VII главе Леонардо излагает действия над обыкновенными дробями. В VIII—X главах изложены приёмы решения задач коммерческой арифметики, основанные на пропорциях. В XI главе рассмотрены задачи на смешение. В XII главе приводятся задачи на суммирование рядов — арифметической и геометрической прогрессий, ряда квадратов и, впервые в истории математики, возвратного ряда, приводящего к последовательности так называемых чисел Фибоначчи. В XIII главе излагается правило двух ложных положений и ряд других задач, приводимых к линейным уравнениям. В XIV главе Леонардо на числовых примерах разъясняет способы приближённого извлечения квадратного и кубического корней. Наконец, в XV главе собран ряд задач на применение теоремы Пифагора и большое число примеров на квадратные уравнения. Леонардо впервые в Европе использовал отрицательные числа, которые рассматривал как долг.
«Книга абака» резко возвышается над европейской арифметико-алгебраической литературой XII—XIV вв. разнообразием и силой методов, богатством задач, доказательностью изложения. Последующие математики широко черпали из неё как задачи, так и приёмы их решения. По первой книге многие поколения европейских математиков изучали индийскую позиционную систему счисления. Другая книга Фибоначчии, «Практика геометрии» (Practica geometriae, 1220 год), содержит
разнообразные теоремы, относящиеся к измерительным методам. Наряду с классическими результатами Фибоначчи приводит свои собственные — например, первое доказательство того, что три медианы треугольника пересекаются в одной точке (Архимеду этот факт был известен, но если его доказательство и существовало, до нас оно не дошло).

В трактате «Цветок» (Flos, 1225 год) Фибоначчи исследовал кубическое уравнение , предложенное ему Иоанном Палермским на математическом состязании при дворе императора Фридриха II. Сам Иоанн Палермский почти наверняка заимствовал это уравнение из трактата Омара Хайяма «О доказательствах задач алгебры», где оно приводится как пример одного из видов в классификации кубических уравнений. Леонардо Пизанский исследовал это уравнение, показав, что его корень не может быть рациональным или же иметь вид одной из квадратичных иррациональностей, встречающихся в X книге Начал Евклида, а затем нашёл приближённое значение корня в шестидесятеричных дробях, равное 1;22,07,42,33,04,40, не указывая, однако, способа своего решения.
«Книга квадратов» (Liber quadratorum, 1225 год), содержит ряд задач на решение неопределённых квадратных уравнений. В одной из задач, также предложенной Иоанном Палермским, требовалось найти рациональное квадратное число, которое, будучи увеличено или уменьшено на 5, вновь даёт рациональные квадратные числа.
Последовательность Фибоначчи, известная всем по фильму "Код Да Винчи" - ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:
Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.


В итоге получается такая последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Эту последовательность можно продолжать бесконечно долго. Её суть в том, что каждое следующее число является суммой двух предыдущих.
У этой последовательности есть ряд математических особенностей, которых обязательно нужно коснуться. Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной,
непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Так отношение какого-либо члена последовательности к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы последовательности через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.
К чему всё это? Так мы приближаемся к одному из самых загадочных явлений природы. Фибоначчи по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.
Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение - высшее проявление совершенства целого и его частей в науке, искусстве и природе.
Если на простом примере, то Золотое Сечение - это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b - 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 2,618, а с к b 1,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.
Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.


Изображение: marcus-frings.de


Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.
Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно

Ничего не напоминает?

Фото: ethanhein on Flickr
И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.
Алое многолистный:

Фото: brewbooks on Flickr
Броколи романеско
Фото: beart.org.uk
Подсолнечник:

Фото: esdrascalderan on Flickr
Сосновая шишка:

Фото: mandj98 on Flickr
А если взглянуть чуть подальше, то можно разглядеть последовательность Фибоначчи в недосягаемых галактиках.


И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.
Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама последовательность далека от совершенства, как и всё в этом мире.
Есть предположение, что последовательность Фибоначчи - это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любой последовательности достаточно знать три её члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.
Каждый член золотой логарифмической последовательности явлется степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: ... z-5; z-4; z-3; z-2; z-1; z0; z1; z2; z3; z4; z5 ... Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: ... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост в последовательности обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.
И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?
Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55...

Источник: greenword.ru
Fibonacci
User:Emijrp/Commons/cs/4
File:Leonardo 1863.jpg
File:Leonardo Fibonacci Estatua.JPG
File:Leonardo da Pisa.jpg

@темы: Друзья на mail.ru

---

1 декабря 2012 года

Первое декабря две тысячи двенадцатого года = 435 \ 368 \ 356

435

Впустите любовь Творца в свою жизнь = Дух должен быть дисциплинированным = Крайность – это есть революция = Мы движемся вместе с потоком изменений = Мы дошли до центра очередного лабиринта = Надо прекратить использовать деньги = Наступает время всеобщего прозрения = Не распространяйте негатив даже в шутку = Необходимо изучать цифровое учение = Ноль - потенциальная возможность = Очень сильные выбросы на Солнце = Переход на более высокий уровень вибрации = Привлекайте силу Святого Духа в свой мир = С помощью Словаря узнаёшь новое = Шестьсот шестьдесят шесть = Эволюция - основа совершенного мира = Энергия высочайшей концентрации

Первое декабря две тысячи двенадцатый год = 438 \ 356 \ 368

438

Источник вашего счастья внутри вас = Кардинальные изменения пространства = Концентрация плазменных образований = Магнитом сердца можно привлечь многих = Настало время решительных действий = Не забывайте благодарить своих помощников = Особые требования к дисциплине мысли = Помни: все вместе мы умнее, чем каждый из нас

1.12.2012 (один миллион сто двадцать две тысячи двенадцать) = 537 = Благополучие меряется не деньгами, а радостью = Близнецовые пламёна - фундамент будущей цивилизации = Если меняемся в мелочах - меняемся глобально = Изменилось время и изменились вибрации планеты = Индивидуальный план эволюционного развития = Переход пространства на новый полевой уровень = Преграда делам твоим - в тебе. Там же ищи причины неуспеха = Сделать власть прозрачной и управляемой Богом = Сделать новую, единую духом расу на земле людей = То, что лекарство для одного - то яд для другого = То, что написано пером, не вырубишь топором = Хотеть нужно всё и желать многое, но не для себя = Частота шестьсот шестьдесят шесть = Эволюционировать и совершенствоваться

Первое декабря две тысячи двенадцатого года + первое декабря две тысячи двенадцатый год + 1.12.2012 (один миллион сто двадцать две тысячи двенадцать) = 1410 = Новая эпоха в вашем развитии позволит обучить вас уметь быть Единым Целым, и при этом не терять своей индивидуальности

@темы: Друзья на mail.ru

---

Ира__Булынина: Классные гифки (22 гифки)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

@темы: АНИМАЦИЯ,АВАТАРКИ, Классные гифки (22 гифки)

---

Ира__Булынина: За мной будете? #виноватволандеморт

Вы точно с этим сталкивались ))

@темы: За мной будете? #виноватволандеморт, ВИДЕО

---

Ира__Булынина: Смешные комиксы (30 картинок)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

@темы: СМЕШНОЕ, ПОЗИТИВ, Смешные комиксы (30 картинок)

---

Ира__Булынина: Демотиваторы (30 фото)

Заряд позитива на весь день от подборки демотиваторов.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

@темы: Демотиваторы (30 фото), ПРИКОЛЫ

---

Ира__Булынина: Прикольные картинки (90 фото)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

87

88

89

90

91

92

93

94

@темы: Прикольные картинки (90 фото), ПРИКОЛЫ

---

Северное сияние или Световые столбы?

;Северное сияние" или Световые столбы?

Сегодня под утро жители Екатеринбурга стали свидетелями необычного явления – висящих в воздухе столбов света. Екатеринбуржцы не только провели перекличку очевидцев необычного явления, но и стали строить предположения о том, что бы это могло быть. Несмотря на все высказанные мнения, самой популярной осталась версия «северное сияние».

Такое же явление наблюдалось и в другом городе.Красноярцы сообщили, что видели минувшей ночью «северное сияние» или Световые столбы..Накануне на одном из городских форумов появилось фото, сделанное на территории города, на котором заметно многоцветное сияние на небе. Жители сразу же начали обсуждать странное явление, которое многие восприняли за северное сияние. Однако ученые сомневаются, что это северное сияние.Но вразумительного обьяснения дать не могут. Как пояснил ИА KNews кандидат физико-математических наук, доцент СФУ Николай Паклин, в Красноярском крае северное сияние можно увидеть, например, на Таймыре, но в самом Красноярске — вряд ли.





источник

@темы: Непознанное, Загадки природы, Аномальные явления, Друзья на yandex.ru, ya.ru:author:162549541, Полярные сияния, Световые столбы, ya.ru:text

---

«Кьюриосити», возможно, открыл жизнь на Марсе

GISMETEO.RU: «Кьюриосити», возможно, открыл жизнь на Марсе | События

Марсоход «Кьюриосити» высадился на поверхность Марса 6 августа 2012 года. Он представляет собой автономную химическую лабораторию, способную анализировать состав почв и компоненты атмосферы. На аппарате установлены 10 научных инструментов общей массой 80 килограммов.

© JPL-Caltech | NASA

Чарльз Элачи, глава Лаборатории реактивного движения НАСА, на конференции в Риме заявил, что «Кьюриосити» обнаружил на Марсе простые органические молекулы, являющиеся необходимым условием для возникновения жизни. Однако ученый уточнил, что это пока предвариательные данные, которые необходимо проверить. Окончательные результаты будут объявлены в начале декабря в Сан-Франциско.

Чарльз Элачи, глава Лаборатории реактивного движения НАСА © Phil McCarten | Reuters

Директор Лаборатории реактивного движения также подчеркнул, что марсоход не имеет на борту аппаратуры, способной обнаруживать живые организмы, но он в состоянии определять присутствие органических веществ в пробах грунта или атмосферы.

http://www.gismeteo.ru/news/sobytiya/kyuriositi-vozmozhno-otkryl-zhizn-na-marse/

@темы: Космос, Непознанное, Жизнь на Марсе, Друзья на yandex.ru, Освоение Космоса, Марсоход, ya.ru:author:140155698, ya.ru:text, Марс

---

Ира__Булынина: Удивительные снимки: жидкости и всплески (10 фото)

Давайте посмотрим, какие интересные снимки можно сделать при помощи такой сложной установки для фотосъемки.
Удивительные снимки!

1

2

3

4

5

6

7

8

9

10

@темы: КАРТИНКИ,ФОТО, Удивительные снимки: жидкости и всплески (10 фото)

---

Ира__Булынина: Массовое ДТП, в котором пострадало 140 автомобилей (9 фото)

В штате Техас произошло одно из крупнейших ДТП в 2012 году.
По официальной информации, полученной от полиции,
в этой аварии пострадало более 140 автомобилей, а погибло 2 человека.
Более 80 человек получили травмы, а 51 человек госпитализирован.

1

2

3

4

5

6

7

8

9

@темы: КАРТИНКИ,ФОТО, в котором пострадало 140 автомобилей (9 фото), Массовое ДТП

---

ОБО ВСЁМ - Обсуждения

i-zu2009 поделилось ссылкой

ОБО ВСЁМ - Обсуждения

У многих народов есть своя легенда о своей Атлантиде.

@темы: Аномальные зоны, Непознанное, Загадки природы, Аномальные явления, Загадки истории, Загадки человека, Друзья на yandex.ru, ya.ru:author:79990778, ya.ru:link

---

Ира__Булынина: Прикольный розыгрыш с ярлыками на рабочем столе (3 фото)

Очень забавный розыгрыш, который вы можете сделать
своими руками всего за 5-10 минут свободного времени
Обязательно смотрим, как его можно осуществить.

1

2

3
Отсюда

@темы: ДЛЯ КОМПЬЮТЕРА, Прикольный розыгрыш, с ярлыками на рабочем столе (3 фото)

---

Astropilot - Hidden Planet (HD)

Спокойной ночи всем и приятных снов!!!
Dominika.

@темы: Космос, Медитативная музыка, Загадки человека, Друзья на yandex.ru, Загадки сознания, ya.ru:author:148104579, ya.ru:text, Видео, Астрал, Медитация

---

Ира__Булынина: Переделайте фото, чтобы я танцевал с мужиком (27 фото)

Очередное творение креативных фотожаберов из социальных сетей.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

@темы: Переделайте фото, чтобы я танцевал с мужиком (27 фото), ПРИКОЛЫ

---

Ира__Булынина: ТОП-10 фактов о себе (10 фото)

Очень интересные факты и информация о человеческом теле,
которые вы точно не знали до сих пор.

1

2

3

4

5

6

7

8

9

10
Отсюда

@темы: ИНТЕРЕСНОЕ, ТОП-10 фактов о себе (10 фото)

---

Свежий ветер в космологии

"Внешние признаки явлений не должны связывать суждений ученого, у него не должно быть излюбленной гипотезы, он обязан быть вне школ и не иметь авторитетов. Он должен относиться почтительно не к личностям, а к предметам".
Фарадей

Космология - раздел астрономии, изучающий свойства и эволюцию Вселенной в целом. (Википедия)

Последние годы в этой науке ощущается острый дефицит новых идей, парадигм и концепций. Прямое следствие этого - все более возрастающий объем неразрешаемых проблем. Как не парадоксально это выглядит, но мощнейшая техническая поддержка наблюдательной астрономии только усугубляет ситуацию. Развитие познания Вселенной все более стопорится рассогласованностью теорий и фактов. Причин тому много, в том числе и чисто психологическая.

Много ученых, положив многие годы жизни, "создали" свое имя и построили свою карьеру, развивая ныне доминирующую модель мироздания. Теперь принять что-то новое, совсем новое, для них очень сложно, ведь придется смириться с тем, что многие усилия были напрасными. А это действительно не просто, ведь ученым, как и всем остальным людям, присущи общечеловеческие слабости. На эту проблему необходимо смотреть по-другому, ведь в науке отрицательный результат, по своей значимости, часто не уступает положительному. Стремление к истине это движение по лабиринту - правильный путь один, а ошибочных множество. Но чтобы понять, что какое-то направление ошибочно - туда надо зайти и обследовать все "углы и щели". Так что напрасных трудов в науке нет и всё по крупицам собранное обязательно пригодится, а удача нужна всем!

Предлагаемая работа является по сути авторской интерпретацией фактов, наблюдений, гипотез, выводов созданных профессиональными учеными. Автором движет исключительно любознательность, а целью является истина.

Куда бы вы не обратили свой взор через достаточно большой телескоп, везде наблюдается приблизительно одно и то же - хаотичное нагромождение самых разнообразных галактик. Их так много, что подсчитать, даже приблизительно, невозможно ведь с появлением новых, более мощных инструментов, удается обнаружить новые далекие галактики, которые ранее наблюдались какими-то невыразительными пятнышками. Предполагается, что в обозримой Вселенной их можно было бы насчитать несколько сотен миллиардов.

Все они, как утверждает господствующая гипотеза мироздания именуемая "Большой взрыв" (БВ), произошли от какого-то спонтанного, непреднамеренного саморасширения некой субстанции, именуемой сингулярность. Случилось это, как полагают, довольно давно, где то 13 млрд. лет тому назад и теперь, как утверждают теоретики, чем глубже мы заглядываем в космос, тем более молодыми мы наблюдаем космические объекты. Такое утверждение выглядит как-то малоубедительным, точнее говоря совсем не убедительным ввиду того, что оно основано на одном единственном наблюдательном факте который можно трактовать и по-другому. Имеется ввиду красное смещение спектра далеких объектов. Было бы более убедительно, если бы были предоставлены и другие доводы в доказательство молодости глубокого космоса.

Довольно давно, когда меня еще "терзали" мысли о возможности такого сценария сотворения мира как БВ, я задал себе вопрос - как же должны выглядеть ранние галактики, которые начали формироваться из динамично расширяющегося вещества? Поразмыслив, я пришел к конкретному выводу. Ход мыслей был приблизительно таким:
1) любая частица в старых галактиках одновременно участвует во множестве движений. Действительно, любой предмет, который вы видите совершает суточное вращение вместе с Землей, годичное вокруг Солнца, галактическое в сложном "полете" вокруг ядра галактики, а все это вместе в каком-то движении в скоплении и сверхскоплении галактик.
2) любая частица вновь формируемой галактики, которая ранее получила импульс движения скажем при взрыве, может одновременно участвовать не более чем в трех движениях одновременно.
- прямолинейного, от источника импульса
- собственного вращательного
- приобретаемого вращательного вокруг центра вновь формируемой галактики.

Исходя из этих соображений был сделал вывод, что вновь формируемая галактика, из такого вещества, может быть только дисковидной формы со строго определенной ориентацией оси своего вращения – по направлению движения. Если ось вращения и направление движения не будут совпадать, то частицы этой галактики в своем движении вокруг ядра будут испытывать знакопеременные ускорения, а это уже является прямым нарушением закона сохранения энергии. И если в дальнейшем, какие-то возмущающие факторы будут приводить к отклонению оси вращения от направления движения, то инерционность частиц будет возвращать ситуацию к исходному состоянию. Этот возврат, думаю, должен приводить к некоторому утолщению диска галактики.

На фото: Похожие на разноцветные леденцы галактики заполняют область глубокого обзора телескопа Хаббла - одно из проникающих наиболее далеко во Вселенную оптических изображений, полученных за историю человечества. Самые слабые объекты, блеск которых составляет 30 звездных величин (примерно в четыре миллиарда раз слабее звезд, видимых невооруженным глазом) - это очень далекие галактики. Они показывают, как выглядела Вселенная в далеком прошлом, когда с момента Большого взрыва не прошло еще и миллиарда лет.

Нет сомнения, что это очень глубокий космос. Чтобы получить это изображение была проделана большая работа и результаты впечатляют. Но даже беглого взгляда на эту фотографию достаточно, чтобы понять ошибочность утверждения о молодости даже, если хотите, детстве, изображенных там галактик.

Если бы на этом фото были действительно все галактики молодыми, то они выглядели бы как корзинки цветущих подсолнухов на поле. Здесь же мы видим типичный участок Вселенной с галактиками разнообразных форм и хаотичной ориентацией осей их вращения.

Настоящая работа является дальнейшим развитием физической идеи устройства квазара, опубликованной в журнале "Наука и Техника" №1 2010г. и на сайте "Астрогоризонт" в статье "Новый взгляд на самые мощные процессы во Вселенной…".

Далее предлагаются к рассмотрению, казалось бы, совершенно не имеющие ничего общего между собой, модели образования кольцевых галактик и образования войдов ( void - англ. пустота).

Теперь все по порядку. Что же мы знаем о кольцевых галактиках? Ну прежде всего, их немного. При удачной ориентации относительно земного наблюдателя мы можем видеть удивительной красы звездный остров, такой как галактика "Колесо телеги".

На фото: Обод галактики представляет собой огромную кольцевую структуру диаметром более 100 тысяч световых лет, состоящую из областей звездообразования, в которых находятся исключительно яркие, массивные звезды.

Когда галактики сталкиваются, они проходят друг сквозь друга, а составляющие их звезды не сталкиваются. Однако эта кольцеобразная форма возникла в результате гравитационного разрушения, вызванного пролетом меньшей галактики сквозь большую. При этом произошло сжатие межзвездных газа и пыли, вызвавшее распространение волны звездообразования, подобное тому, как разбегаются волны по поверхности пруда.

Это составное изображение в искусственных цветах галактики Колесо Телеги получено космическими обсерваториями. Данные рентгеновской обсерватории Чандра показаны фиолетовым цветом, ультрафиолетовое изображение со спутника GALEX (Исследователь эволюции галактик) - голубым, картинка в видимом свете, полученная космическим телескопом Хаббла - зеленым и инфракрасное изображение с космического телескопа Спитцера - красным.

На ободе этой галактики видно очень много ярких голубых звезд. Это свидетельствует об очень интенсивном периоде звездообразования, который прошел не позднее полумиллиарда лет тому назад. Во всяком случае, это предельный срок "жизни" голубых гигантов, которыми как раз и являются эти звезды. В средней части, возле ядра, звезды поменьше и потускнее. Встречаются кольцевые галактики с распадающимся ободом, фрагментированные большими скоплениями звезд в этом ободе, а так же с ассиметричным расположением светящейся материи внутри, которая ассоциируется с ядром.

Утверждение о том, что правильное, симметричное кольцо может образоваться в результате столкновения галактик крайне неубедительно, хотя и полностью исключать такой вариант все же рановато. Существует множество фотографий гравитационно-взаимодействующих галактик. Всегда, при тесном сближении, полностью разрушалась их первоначальная структура. Позже, когда уже "пролетев" одна сквозь другую, они все же еще продолжали взаимодействовать посредством перемычек светлой материи. Похоже, что предположение о столкновении было сказано в основном потому, что надо было что-то сказать.

Вселенная, в сравнительно небольших объемах, довольно неоднородна. Галактики группируются в скопления и сверхскопления, которые формируют в пространстве огромные суперкластеры. Между ними расположены не менее огромные, но совершенно пустые участки пространства – войды Размеры этих пустот очень большие – от десятков до сотен миллионов световых лет и занимают они приблизительно половину видимого объема Вселенной. Часто они "выглядят" почти правильной пустой сферой. Как-то приемлемо объяснить такое перераспределение вещества в пространстве не получается, и вероятно из-за этого космологи не любят обсуждать эту тему.

На фото: Суперкластеры и войды.

Тема все же интересная, поэтому не претендуя на полноту решения проблемы, предлагаю посмотреть на эту загадку по-другому. В моем представлении и кольцевые галактики и войды образуются в результате одинаковых, но разной мощности, процессов.

Представим себе планетарную систему. Представим, что центральная гравитирующая масса, в результате какого-то процесса потеряла часть своего вещества. Что произойдет? Думаю, ответ очевиден - у всех планет этой системы увеличится размер орбиты. Теперь тоже самое, только с галактикой. Ну, в общем то, принципиальной разницы нет. Ну, а если это будет скопление галактик? Да, все то же самое, ведь и там наблюдаются центральные гравитирующие массы типа Великого аттрактора (attract - англ. притягивать). Теперь нужна подходящая физическая идея по удалению центральной гравитирующей массы или её части за пределы системы.

Как догадывается читатель, сюда хорошо подходит, предлагавшаяся ранее, модель квазара. Как мы знаем, абсолютное большинство квазаров совмещено с центральными областями галактик. "Работающий" квазар оказывает очень сильное воздействие на материнскую галактику, разбрасывая веером свое вещество в галактической плоскости. Скорость движения этого вещества соизмерима со световой, да и его колличество тоже значительное. Это подтверждается наблюдениями в квазарах "звездного ветра", дующего из центра в плоскости галактики. Извергаемое вещество разрушает звезды и оттесняет пыль и газ к периферии. Ослабляющаяся гравитационная связь с ядром галактики тоже способствует очищению внутренних ее областей и формированию "обода". Сформировавшаяся таким образом волна сжатия на фоне изобилия вещества для звезд и создает то великолепие, которое мы наблюдаем. Если одной фразой, то кольцевые галактики - это постквазарные галактики.

С непринципиальными отличиями, приблизительно так же образуются и войды в скоплениях галактик, но масштабы этого процесса должны быть куда более грандиозными, и для образования войда нужен уже суперквазар. Скорее всего нечто подобное происходит сейчас в скоплении галактик MS0735.6+7421, где обнаружено колоссальное извержение с характерным, для моей гипотезы, распределением вещества. Время образования войдов огромно - десятки млрд.лет, поэтому следов каких либо извержений обнаружить уже не удается.

Недавно я обнаружил в сети любопытную информацию, опубликованную в апрельском номере журнала Astrophysical Journal Letters за 2006г. которая, собственно, и подтолкнула меня к написанию этой статьи.

Еще с 90х годов астрономы уже знали, что галактические кластеры в виде нитей и плоскостей окружают полости между ними. Международная команда английских и испанских астрофизиков провела обследование 470 войдов. Специальные методы обработки материалов наблюдений помогли выявить удивительную закономерность. Оказывается, что спиральные галактики, подобные Млечному пути, расположены вокруг этих войдов, как бусины в ожерелье, со своими осями вращения согласованными с нитью, как бы связывающей эти галактики. Ученые пришли к выводу, что такая ориентация осей вращения галактик оказалась значительно более частой, чем можно было бы предположить, исходя из вероятностных теорий. Было подсчитано, что вероятность не случайности такой ориентации составляет 99,7%.

Какие же выводы и предположения можно сделать из этого наблюдения, исходя из вышеизложенного?
1) Такая синхронная ориентация осей вращения скорее всего связана с вращением этих галактик вокруг войда.
2) Можно предположить, что подобный этому "хоровод" существовал и ранее, еще до начала роста войда, разумеется с меньшим диаметром орбиты.
3) Можно предположить, что в окрестностях войда должно быть много спиральных галактик, сформировавшихся из вещества суперквазара. Те из них которые не участвуют в движении вокруг войда, думаю, должны иметь ориентацию оси своего вращения на центр этой полости и это тоже должно быть значительно более частым, чем исходя из вероятностных теорий. Искать их, скорее всего надо, в основном, в направлении перпендикулярном плоскости "хоровода".
4) Возможно в центре войда есть еще значительная гравитирующая масса.

Часто сторонники альтернативных взглядов склонны придавать слишком большое значение критике общепринятых теорий. Они надеются, что, наглядно показав трудности этих моделей, можно добиться отказа от них. Но, как утверждал философ науки Имре Лакатос - теорию не могут уничтожить ни эксперимент, ни парадокс. Теорию сбрасывает с "пьедестала" только новая, лучшая теория.

Как может отметить читатель, и в этой статье, и в предыдущей не подвергалась критике стандартная модель мироздания. В этом нет надобности, поскольку предлагается новая система взглядов на космологию, и в которой большинству старых гипотез не находится места.

Построенная на одном единственном, вполне логичном, предположении модель квазара повлекла за собой образование ряда концепций некоторых процессов во Вселенной:
1) Был предложен процесс образования химических элементов, который наряду с процессами в звездах и создает наблюдаемое разнообразие и соотношение этих элементов. Как это не удивительно, но эта концепция обрела экспериментальное подтверждение, которое в значительной мере подтвердило предположение о регенеративной функции квазаров.
2) Была предложена модель образования гамма – всплесков, с разнообразными их временными профилями.
3) Предлагается механизм образования кольцевых галактик которые, с большой долей вероятности, являются постквазарными галактиками.
4) Предлагается концепция перераспределения вещества во Вселенной и образования войдов.

Для образования по-настоящему большого войда, как отмечалось, нужен суперквазар, а сверхплотные тела, образующие активный элемент в виде двойной системы, должны накопить сверхмассу в этом случае, равную уже многим триллионам солнечных масс.

ЧД растут за счет поглощения малоплотных образований (планеты, газовые звезды, туманности) а так же за счет очень плотных карликовых звезд. Если же сблизятся высокоплотные тела (ЧД, кварковые и нейтронные звезды), то дальнейшее развитие будет зависеть от соотношения масс этих тел. Если разница не очень большая то, как было описано в предыдущей статье, образуется квазар с выбросом джетов. Если же разница будет большая, то образуется квазар без джетов, т.к. режим разуплотнения наступит только у меньшего тела и все извергаемое им вещество будет перебрасываться на более массивное тело. Излучение же, образующееся при разуплотнении, многократно увеличит яркость ядра материнской галактики. Такие объекты астрономы называют галактиками с активным ядром.

Постоянно растущие ЧД в конце концов, в результате медленного, хаотического перемешивания вещества Вселенной, находят себе достойную пару, чтобы дать жизнь новым звездам, планетам и галактикам попутно образовав либо кольцевую галактику, либо войд. Вот так замыкается цепь кругооборота вещества и энергии в природе. Действительно ЧД поглощают вещество обогащенное тяжелыми элементами а при разуплотнении, как показывают наблюдения и эксперименты, образуется в основном водород.

Подытоживая все вышесказанное можно, с большой долей уверенности, утверждать, что Вселенная все же бесконечная, хаотичная и вечная. Для существования такой Вселенной также необходима и темная материя. Поглощая излучение, она поддерживает термодинамическое равновесие на наблюдаемом уровне. Что она собой представляет сказать невозможно, но если предлагаемая концепция устройства квазара близка к реальности, то это могут быть ЧД различной массы.

Феномен "красного смещения" не имеет однозначного объяснения и, вероятно причинами, в комплексе, являются все возможные физические эффекты. Так же нельзя сбрасывать со счетов то обстоятельство, что мы можем чего то не знать, очень важного о свойствах излучения или о свойствах среды его распространения. Или будем считать и дальше космос сверхпроводником для излучения?

Несмотря на очевидный недостаток предложенных взглядов (нет математической их проработки), они все же представляют собой некий базис, на котором можно монтировать фундамент новой космологии. Эта уверенность основана на том, что предложенные концепции создают, все же, более реалистичное представление о мироздании чем стандартная модель и к тому же они не противоречат известной физике, наблюдательным данным и что не маловажно – здравому смыслу. Так же, для их поддержки не нужны какие-то новые сущности типа "темной энергии", расширения пространства и т.д. Эти же концепции позволяют уйти от абстракции сингулярности и явного нарушения принципов сохраняемости.

Завершая, следует сказать и о экспериментах, проведенных в лаборатории "Протон 21". Упорное их игнорирование, основанное на единственном "доводе", что этого не может быть, граничит с неразумным упрямством, которое, по своей сути, ничего общего с наукой уже не имеет.

@темы: Космос, Непознанное, Астрономия, Друзья на yandex.ru, Загадки Вселенной, ya.ru:author:148104579, ya.ru:text

---

"Хаббл" запечатлел "космическую розу"

Телескоп "Хабл" сделал кадр в созвездии Андромеды двух взаимодействующих галактик, напоминающих внешне розу. Фотоснимок опубликовали в честь двадцать первой годовщины начала деятельности "Хаббл" на орбите.

На расстоянии 300 млн. световых лет расположена пара взаимодействующих Arp 273 галактик. Самая крупная из них, располагается сверху UGC1810, имеет вес, пятикратно превосходящий вес малой галактики UGC1813.

На снимке видны следы обильно взаимодействия звездных скоплений. Внешний рукав крупной галактики имеет искривленную конфигурацию, он окружен множеством последовательных молодых ярких звезд голубого оттенка. В верхнем правом углу UGC1810 проявляется спиральная структура, которая напоминает мини-галактику.

По мнению астрономов, кадр свидетельствует о том, что некоторое время назад UGC1813 проскочила сквозь большую UGC1810, однако по краю, а не через центр. Прежде всего, это вызвало её искривление, и в результате столкновения облаков с межзвездной пылью произошло образование новых звезд. Ученых говорят, что подобные процессы зачастую сопровождаются столкновением галактик.

Прежде необычную галактику зафиксировала обсерватория "Джемини" неподалёку от созвездия Рыб. Скопление сформировалось после слияния двух спиральных взаимодействующих галактик. В будущем такая же структура способна образоваться при слиянии Андромеды с Млечным Путём.

@темы: Космос, Непознанное, Чудеса природы, Астрономия, Друзья на yandex.ru, Рисунки Общемирового Информационного Поля, ya.ru:author:137257662, ya.ru:text